Pathfinding to a moving target in evolving terrain

In this post, I'm going to describe how I used direction fields to introduce fast and dynamic pathfinding to a browser game.

I recently published a free browser game, developed in Unity, called Build + Brawl. In Build + Brawl, the player moves their character to avoid swarms of approaching enemies. The environment contains impassable obstacles — some generated at random, some placed by the player — that the enemies must route around as they approach the player. There are off-the-shelf solutions for pathfinding in general using algorithms like A* [1]; however, there were a few quirks to Build + Brawl that pushed me to roll my own solution:

• There may be hundreds of enemies routing to the player at once.
• The enemies all start from different, randomized positions.
• The player character can move.
• The player can add or remove obstacles during the game.
• The game must run in realtime, without lag, single-threaded, in the browser.

Running A* worked fine in a high-resource desktop environment, but introduced noticeable lag in the browser. The next two parts detail how I fixed this.

Part 1: hunting down a moving target

Let's first ignore the fact that the player can add or remove obstacles, and focus on the narrower problem: routing the enemies towards the player, even as the player moves around. There are a few attributes of the Build + Brawl scenario that A* does not fully leverage:

1. The player can only move from one space to the next space. Paths are unlikely to change dramatically as the player moves, and most changes would be in the neighborhood of the player. Recomputing the whole path from start to finish every time the player moves would be inefficient.
2. Every enemy is moving towards the same target. Two enemies that pass through the same cell, even at different times, should follow the same path thereafter (assuming the player has not moved). Treating each enemy as a separate pathfinding entity does not leverage this, since even enemies in similar positions would calculate their paths from scratch [2].

In general, it seemed like there was an opportunity to do some extensive path caching and make minimal updates as the player moves. The approach I settled on was inspired by a direction field [3]:

A direction field, with two paths (in red) from different starting positions
https://courses.lumenlearning.com/calculus2/chapter/direction-fields/

A direction field shows the slope of a function — that is, the direction that function follows — at each point in a grid. What if we could compute something similar for the enemies in our game? What if we pre-computed which direction an enemy in position (x, y) should go, for every possible (x, y)? That way, the pathfinding cost is independent of the number of enemies on screen at a time, since all of them can just check against the same pre-computed direction field.

To build our pathfinding direction field, we'll start by dividing the map into a grid of equal-sized cells. Each cell is going to hold two pieces of data:

• A pointer to one of its neighboring cells. A pointer from cell X to cell Y means "when an enemy is in cell X, its shortest path to the player goes through cell Y next." You can think of this as the "direction" of our direction field. The cell containing the player points to itself.
• A distance value, representing how long the path is from the cell to the player. A distance value of N in cell X means "the shortest path to the player from cell X is N cells long." The cell containing the player has a distance value of 0.

If we have these values for every cell, then we've solved the pathfinding problem: enemies could just check the pointer of their current cell, move to that neighboring cell, and then repeat the process until reaching the player. We have two problems to solve to get these values:

1. Calculating the pointers and distances for every cell at map initialization.
2. Updating cell pointers and distances as the player moves.

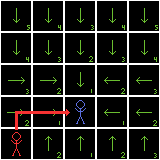
We can make problem (1) simple by assuming there are no obstacles on the map (we'll cover how to add obstacles in Part 2 of this post). Here's our blank grid, with the player at the center:

Because there are no obstacles, enemies can traverse any cell in the grid, meaning each cell should just point towards the player: if the cell is below the player, point to the neighbor above; if above, point below; if to the left, point right; and if to the right, point left [4]. The distance value for each cell would then equal 1 plus the distance value of the neighbor being pointed to.

Unfortunately for us, we're not done yet, because the player won't stay in that cell forever. To handle player movement, we need to solve problem (2). Thankfully, the player can only move one cell at a time. This means that, when the player moves, every cell has a "default" option: take the same route as before, but when reaching the player's previous position, move from there to the player's new position. This default option gives every cell its same pointer, and a distance value 1 greater than before (since it must reach the previous player position, then move one more space). We'll start by updating every cell to use the default route and increment their distance values by 1:

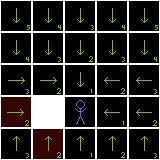
But this default route will not always be the shortest route. For example, if an enemy is below the player and the player moves one cell down, it would be inefficient for the enemy to move up to the player's previous row, then back down to the player's new row:

We need to find all of the cells that have a new fastest route to the player. To start, all of the cells adjacent to the player's new position have a new route: just point to the player! We can update all of their pointers and set their distance values to 1:

We put each of these updated cells into a queue (marked in yellow). Let's call this queue the sellers, because our cells are going to be offering some deals. One at a time, we dequeue cells, and the dequeued cell offers a deal to its neighbors: "Point to me! Then your distance will be only 1 plus my distance!"

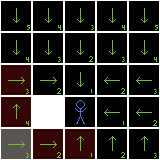
Let's say the cell to the right goes first:

That cell (in gray) announces to its neighbors (in purple), "if you point to me, your distance to the player will be only 2!" Each of those neighbor cells check against their current distance value. If the offered distance is shorter than their current distance, they take the deal: the neighbor cell points to the dequeued cell and sets its distance value to 1 plus the dequeued cell's distance.

In this case, the only cell to take the deal is the cell to the right, which previously pointed to the row above the player:

The updated neighbor now has a shiny new deal to offer its neighbors, so it joins the queue and waits its turn. This process continues until the sellers queue is empty; for now, the space below the player is up next. It offers its deal — a distance of 2 — to its neighbors, but no one is interested, since their distances are already equal to 2:

The space to the left gets dequeued next:

The cell to its left takes the deal and joins the queue:

The cell above the player makes its offer, but no takers:

After patiently waiting its turn, that updated cell on the far right gets dequeued. None of its neighbors are interested:

And finally, the updated cell on the far left gets dequeued. Likewise, no takers:

The queue is now empty, meaning every cell has no better pointer option than its current selection. At this point, the grid is fully updated, and every cell once again knows the shortest path from itself to the player. That enemy starting from the bottom corner now has a much more reasonable route:

As we saw here, many cells will not need to be checked at all in this approach, which avoids a full grid update every time the player moves.

Part 2: adding and removing obstacles

In Part 1, we built a direction field that points towards the player as they move around the map. But we assumed there were no obstacles blocking enemy movement; if that were always the case, we could just have enemies always move in a straight line towards the player! In Build + Brawl, the player can add and remove obstacles throughout the game. As obstacles are added and removed, the shortest paths to the player might change, as routes open up or become blocked off. For instance, if we place an obstacle to the left of our player, the path we found in Part 1 no longer works:

We need to update our direction field to route around the obstacle:

Let's first figure out how to handle the addition of a new obstacle [5]. Naively, we could recompute the pointer and distance for every cell from scratch whenever an obstacle is placed. Intuitively, however, most cells shouldn't need to be updated: we should only need to update cells whose shortest path eventually led through the now-impassable one [6].

To do this, we can work backwards from the impassable cell: we find all cells that point to it, then find all cells that point to those, and so on, until we've found every cell that eventually routed through the impassable one. We then want to indicate that we no longer know the shortest path for those cells, so we unset their pointers and set their distance values to infinity.

In the above example, two cells point to the now-impassable one:

So we unset their pointers; one cell pointed to one of those:

So we unset its pointer as well:

Once that's done, we have a lot of cells pointing to nowhere. We need to find their new shortest paths to the player and reset their pointers. We start with a new queue, containing all of the unset cells. Where the queue in Part 1 was full of sellers offering sweet deals to their neighbors, this queue is full of buyers: each cell in the queue is going to look for the best offer among its neighbors.

As long as the queue is nonempty, we dequeue a cell from it. We'll start with the cell to the left of the obstacle:

That dequeued cell finds the neighboring cell with the shortest distance value. The dequeued cell can now decide: should I point to this neighbor? If so, the dequeued cell's distance would be 1 plus the neighbor's distance. If that's shorter than the dequeued cell's current distance, then it takes the deal and updates its pointer and distance value accordingly. In this case, the best deal is to go up, taking a distance of 4:

Whenever a cell updates, its neighbors catch wind of the sweet deal and join the buyers queue, in case they might get a shorter path by routing through their newly-updated neighbor:

Next, the cell below the obstacle is dequeued; it finds a path of length 2:

The cell in the bottom-right is dequeued. It has a choice between a path of length 3 and a path of length 5, so it chooses the shorter path:

There are a few cells remaining in the queue, but none find a better deal, so nothing else gets added as we iterate over them. At the end of the process, every cell whose path was ruined now has a new pointer, and all other cells have been given a chance to route through these new paths.

The last piece of our pathfinding puzzle is updating the distance field when an obstacle is removed. There are two problems to solve when this happens:

1. To which neighbor the now-passable cell should point
2. Whether any other cells should route through the now-passable cell

Problem (1) is simple: check the now-passable cell's neighbors, find the neighbor with the shortest distance value, and point to it. If we were to remove the obstacle added above, this is simple, as the neighbor with the shortest distance is the cell containing the player:

Problem (2) can be solved using a method very similar to the sellers queue in Part 1:

• The now-passable cell "offers" itself as a route for all of its neighbors:

• If the neighbor would get a shorter path by pointing to the now-passable cell, it does so:

• Any updated neighbors offer themselves to their neighbors, and so on, until no cells are updated:

We end up with a direction field that once again contains the shortest routes to the player!

Result

The direction field approach produced no noticeable lag in the browser, allowed the game to scale to more enemies, and most importantly, was really fun to figure out. Hopefully this can be helpful to anyone encountering a similar problem!

Footnotes

[1] I tried Aron Granberg's A* Pathfinding Project. It's definitely a high-quality library, and was easy enough to use, but I couldn't get the lag down when running single-threaded in-browser.

[2] I tried using A* Pathfinding Project's multi-target pathing, which was better than separately pathing every enemy, but this still caused a lag spike whenever it ran.

[3] The approach I ended up using is very similar to a Dijkstra map, a pathfinding tool from roguelike games, which I discovered as I was writing this. As far as I could tell, my approach extends a Dijkstra map to handle minimal updates as the target moves and obstacles update.

[4] In practice, I also allow diagonal connections. These connections are the same as cardinal direction connections, except they impose an additional distance value of sqrt(2) instead of 1. You also need to be careful that connections can't cut through obstacles placed kitty-corner to one another. Otherwise, the same algorithm works just as well, it's just a bit harder to walk through it that way.

[5] This algorithm assumes that placing an obstacle does not created a disconnected component of the grid, meaning an enemy in any (non-obstacle) space can reach the player. Preventing that was a tricky problem I might cover in a future post.

[6] If you're implementing diagonal movement, a route is also ruined if there's an obstacle orthogonal to the direction of the pointer, even if the start and end cells themselves are clear. This prevents clipping through obstacles diagonally.